Understanding Maximum Parsimony

Conceived by Olof Karlberg and Mikael Thollesson (c) The authors(s) and SweLL, 2001

The aim of maximum parsimony is to find the shortest tree, that is the tree with the smallest number of changes that explains the observed data.

An example:

position
1	2	3
Sequence1	T	G	C
Sequence2	T	A	C
Sequence3	A	G	G
Sequence4	A	A	G

First draw all the possible trees. For four sequences there are three possible unrooted trees.
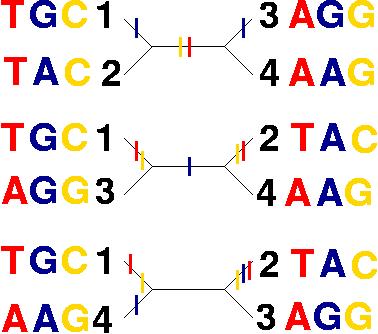
Then consider each position separately:

• Position 1: Only one change is introduced if sequences 1 and 2 are grouped, while two changes will be necessary if sequences 1 and 3 or 1 and 4 are grouped.
• Position 2: Only one change is introduced if sequences 1 and 3 are grouped, while two changes will be necessary if sequences 1 and 2 or 1 and 4 are grouped.
• Position 3: Only one change is introduced if sequences 1 and 2 are grouped, while two changes will be necessary if sequences 1 and 3 or 1 and 4 are grouped.

Then, from the three possible unrooted trees,try to find the tree that needs the fewest changes to explain the data:

• If 1 and 2 are grouped a total of four changes are needed.
• If 1 and 3 are grouped a total of five changes are needed.
• If 1 and 4 are grouped a total of six changes are needed.

Hence, the shortest tree is ((1,2)(3,4)).

Try to find the shortest tree by hand with the following sequences:

1. CAGATCGCAGTTAGTTCCTAA

2. CGGACCGCCGGTAGTACGCAG

3. CAGATCGCCGGTAGTACGTAA

4. CGGACCGCAGGTAGTTCCCAG

Try first with equal weights for all substitutions and then with transversions at twice the cost of transitions.

The answer should contain the branching order (use parantheses) and length for the shortest tree(s).